|
|
|
ORIZZONTE |
| testo di Ivonne Favro
Che cosa è? |
|
|
L'orizzonte è quella linea immaginaria oltre la quale non riusciamo a vedere a causa della curvatura
della terra dovuta alla sua forma pseudosferica. In passato questa evidenza era riscontrata osservando
la proiezione dell’ombra della Terra sulla Luna durante le eclissi; oggi le cose sono più facili poiché
le foto scattate dallo spazio ben ci mostrano questa peculiarità comune a tutti i pianeti.
Altra evidenza curiosa, che forse non tutti hanno notato, consiste nell’osservare l’ombra della Terra
che si proietta progressivamente nel cielo, a Est sopra l’orizzonte, quando il Sole è appena sceso
completamente a Ovest; non più impegnati ad osservare il romantico tramonto, si vede muovere un grande
arco tondeggiante che ci dice che il nostro pianeta è sferico. |
|
|
Fino a quale distanza riusciamo a vedere? |
|
|
Fatte queste premesse sembrerebbe che l’orizzonte
debba essere un limite invalicabile alla nostra "portata ottica", ma non è così perché
può intervenire in nostro aiuto la rifrazione della luce. Tale fenomeno non è altro che una deviazione
del percorso della luce che segue una linea non più retta ma spezzata; questo si verifica grazie alle
diverse condizioni degli strati gassosi dell’aria dovute alla diversa densità che è strettamente correlata
a temperatura, umidità e quota.
In condizioni particolari quindi può capitare di vedere ciò che normalmente ci è precluso.
Vi sono purtroppo alcuni elementi di disturbo per una buona visione:
la prima è la foschia che riduce il contrasto e quindi la definizione dell’oggetto osservato,
la seconda è rappresentata dalle particelle chiamate aerosol ma dette comunemente pulviscolo. Sono
proprio queste particelle i principali ostacoli alla propagazione della luce in atmosfera, pertanto le migliori
condizioni di visibilità si hanno quando c'è poco aerosol e bassa umidità.
Da noi la visibilità migliora con vento di Tramontana che apporta aria secca e pulita da Nord, tanto
che è facile avere visibilità di oltre 100 km.
|
|
|
Dove è posizionato l’orizzonte? |
Oltre alle condizioni di base, riportate
in premessa, va sottolineato che la distanza dell'orizzonte è direttamente proporzionale all'altitudine
dell'osservatore rispetto alla superficie terrestre.
Più ci troviamo in alto, più l’orizzonte si allontana permettendoci una più ampia visibilità. |
|
|
|
|
|
|
|
 |
|
|
|
|
|
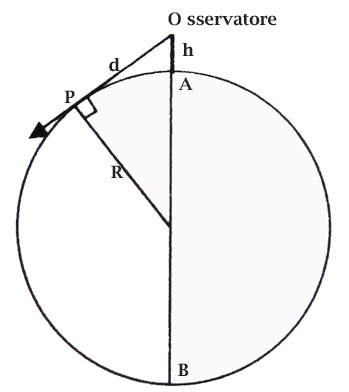
R = raggio terrestre = 6350km
OA = h = altezza dell'osservatore
OP = d = distanza dell’orizzonte visto dall'osservatore (tangente al livello del mare)
|
|
|
|
|
|
|
|
in P si forma un angolo retto, applicando il
Teorema di Pitagora avremo:
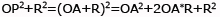
da cui si ricava
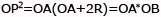
riscrivendola quindi
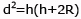
ma essendo h una misura trascurabile rispetto a R, posso scrivere
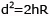
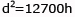
ovverosia
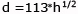 |
|
|
|
|
|
| Questo risultato rappresenta la distanza minima
dell’orizzonte; va tenuto però in considerazione il fatto che, per effetto della rifrazione della luce
passante fra strati di atmosfera non omogenei, questa misura tende ad aumentare, in altre parole la
linea d'orizzonte si allontana e noi possiamo "vedere di più". |
|
|
|
|
|
Riassumendo possiamo dire che, ad esempio,
per un osservatore:
posto su una spiaggia, con gli occhi ad un'altezza di 1,60m dal suolo, il suo orizzonte sul mare
si trova a circa 4,5km di distanza;
posto su di un faro alto 60m il suo orizzonte si trova a 28km (113*0,060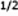 ) )
posto in Liguria, su un'altura di 50m, riesce a vedere i monti della Corsica che si trovano ad una distanza
di 200Km;
posto sulla cima della tour Eiffel (33,5 metri di altitudine + 300 metri d’altezza) l’orizzonte,
riferito al livello del mare, si trova a 65km di distanza. |
|
|
|
|
Da una altura riesco a vedere fino alla linea
d’orizzonte intesa sul livello del mare, ma se oltre tale linea ci fosse un’altra altura riuscirei a
vederla?
Fino a che distanza riesco a vederla in funzione della sua altezza?
Applicando due Teoremi di Pitagora non è difficile:
è sufficiente sommare le singole
distanze d’orizzonte da ciascuna delle due alture. |
|
|
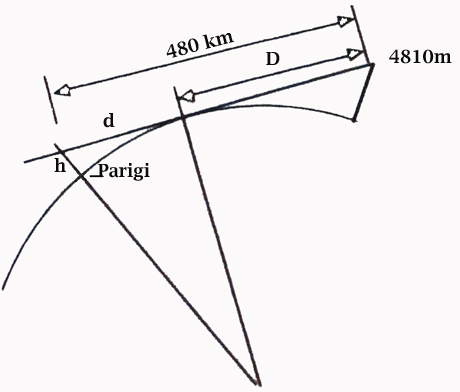
Allora ... da Parigi, sulla Tour Eiffel, riusciremmo a vedere il monte Bianco alto 4810m? |
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
Sappiamo che la distanza tra i due, in linea d'aria, è di 480km
D risulta 248km ( teorema di Pitagora D = 113*4,8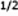 ) )
avevamo detto che la distanza dell’orizzonte dalla Tour Eiffel è di 65Km
senza tener conto della rifrazione della luce, dalla Tour riuscirei a vedere il monte Bianco
soltanto se si trovasse a una distanza di 313Km (248+65) oppure, riuscirei a vederlo soltanto se la
Tour fosse alta 4215m
Essendo
d = 480-248 = 232km
h = (232/113)² = 4,215km |
|
|
|
|
|
|
..è l'altezza richiesta per poter vedere il monte Bianco da Parigi!!
|
|
|
|
|
|
Naturalmente tutti questi ragionamenti sono
validi solo se in perfette condizioni di luminosità e di trasparenza dell’atmosfera, anche se la rifrazione
atmosferica, dovuta a passaggi della luce in strati diversamente omogenei, esalta le ampiezze della visuale. |
|
|
|
|
|
Per quanto concerne la curvatura terrestre va
ancora aggiunto che non dobbiamo farci ingannare dagli effetti fotografici nelle fotografie scattate
con "grand’angolo". Si può notare, in alcuni casi, la "falsa curvatura" della linea
dell’orizzonte determinata
dal tipo di inquadratura:
se prendiamo un’inquadratura con "poco cielo" vedremo un orizzonte che sembrerà un dosso,
se prendiamo un’inquadratura con "tanto cielo" vedremo un orizzonte concavo.
Sono effetti parassiti prospettici, distorsioni ottiche, dovuti al fatto che le visuali non sono
state situate correttamente sull’asse ottico dell’apparecchio fotografico, perciò la linea tondeggiante
non evidenzia assolutamente la curvatura terrestre.
|
|
|

